“Golden Escalante”
© 2022 Douglas McKenna. All rights reserved.

Mathemaesthetics was founded in 1988 by Doug McKenna, a software developer and mathematical
artist who delights in recursive geometries.
In addition to his work as a software developer--itself a form of mathematical art--McKenna
has for over 40 years created works in his chosen medium of fractal tile designs, space-filling
curves, and other recursive or self-referential geometries. These constructions would have been
impossible to accurately create before the computer age.
McKenna is a pioneer in recursive designs. He began creating geometric fractal art in 1977,
on early, low-resolution bitmap
displays at Yale University. In 1978, he began drawing geometric fractals on
a computer-controlled pen plotter using his own custom software and drivers. Prior to the advent of
commonly available algorithms and languages like PostScript for coloring and filling arbitrary complex areas,
McKenna would painstakingly color his fractal designs by hand, with a nib pen and India ink (for which only a razor
blade worked as an “eraser”!).
As a result of his growing portfolio of illustrations, constructions, as well as his discovery of a
some fundamental space-filling curve constructions, during 1980-81 McKenna hired on at IBM Research as one of
Prof. Benoit Mandelbrot's two full-time computer graphics illustrators, where he designed and coded
many high-resolution
pictures of geometric fractals for Mandelbrot's influential treatise, The Fractal Geometry
of Nature. The book contains ten black & white
Plates by McKenna (see p. 444 for partial list), and dozens of smaller illustrations visually explaining the
geometric etymologies of the larger constructions Mandelbrot used to illustrate fractal fundamentals. These
illustrations were created on experimental IBM phototypesetting
equipment of the day, often pushing the computer graphics software of that time to its limits.
McKenna went on to have one of the very first fractal art shows in 1981,
at the Capitol Children's Museum in Washington, DC. Several of his Dragon Curve variations appeared
in Smithsonian Magazine's first 1983 article on fractals. In 1984, he had a successful one-person
show, entitled "Mathemaesthetics", on Boston's Newbury Street. Yale University's
first fractal
art show (1985) featured several dozen of McKenna's early "plottery".
During the 1990s, McKenna concentrated on selling Mathemaesthetics' Resorcerer and other software products. With
the advent of personal computers running at speeds 1000 times faster than in the late 1970s, McKenna's
20-year quest to enumerate square-filling Peano Curve constructions hit paydirt when in 1998
he successfully enumerated over 20 million new space-filling recursive tile designs. This opened up
a visually rich combinatoric space which McKenna is currently exploring for aesthetically or algorithmically
interesting designs.
The late computer graphics pioneer Ken Knowlton once rendered McKenna's visage with
a self-referential portait, drawn
using a single set of connected lines based on several space-filling curve constructions McKenna discovered via an exhaustive
search in 1978.
Each piece is a large, limited edition Giclée print. The Giclée process has come a long way
in the last decade. Giclées are created using archival
quality inks and fine-art, acid-free paper, printed individually at very high resolution
(unlike the low-resolution web samples here on your computer screen).
Giclées are
the basis of a thriving web-based market for artists to sell directly to their customers.
Each print is signed and numbered by the artist, or in McKenna's case, the artist-discoverer.
These prints make fantastic gifts for any mathematically or visually minded person.
They are also a great way
to initiate math or computer science students into the wonders of recursive thinking.
Pricing and Ordering McKenna Prints

“Golden Escalante”
© 2022 Douglas McKenna. All rights reserved.
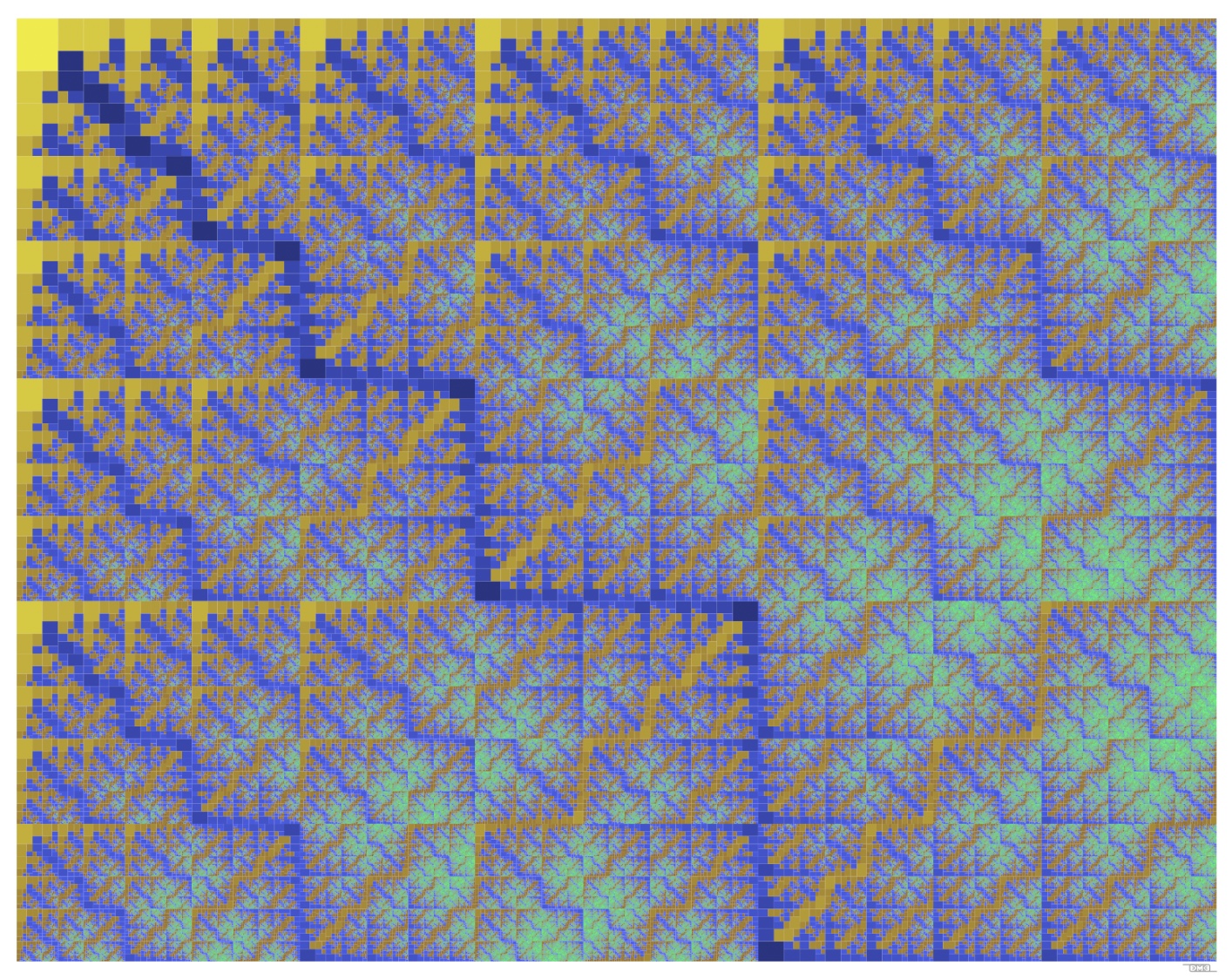
Golden Escalante is a perfectly recursive tiling of the “better golden rectangle” with smaller copies of itself, going down 13 levels. 1,594,323 copies to be exact. Rectangles are colored according to size and orientation (the smallest are green), in order to bring out fractal staircase structures that evoke an aerial view of riversheds in canyonlands of the American southwest, such as the Escalante Staircase area of Utah. This piece is intimately related geometrically to both Golden Gnomon andPhiberspace shown below.
See magnified detail here.
Inquire about ordering a limited edition copy (one size, 40 by 32 inches)

“Filigree from Eleven Dominos”
© 2023 Douglas McKenna. All rights reserved.
Filigree from Eleven Dominos is a combination of a special space-filling curve that overlaps itself while filling a domino, and a fractal pattern in blue that covers exactly half of that domino's area. The filigree pattern built from sequentially connected diagonal line segments has an almost Islamic tiling flavor to it.
See magnified detail here.
Inquire about ordering a limited edition copy (largest size is 60 by 30 inches)

“A Unit Domino”
© 2015 Douglas McKenna. All rights reserved.
Winner of the 2020 Joint Mathematics Meeting's art show's Best Photograph, Painting, or Print category,
A Unit Domino is based upon an artist-discovered “half-domino” space-filling curve.
The drawing comprises some half-million connected line segments, arranged in two perfectly recursive
levels of double-spiral pairs, slowly changing color, in a single, over-one-mile-long self-avoiding
path from lower left to lower right (the lower right square that sticks out is an integral part of
its self-negative structure). The limiting curve covers a self-similar gasket tile with an infinitely
long, almost-everywhere linear border. With an upside-down copy of itself, two such gaskets of unit
area exactly cover a 1x2 domino, without overlap.
See magnified detail here.
McKenna's app/eBook
Hilbert Curves: Outside-In and Inside-Gone explains how
he discovered these beautiful constructions, and thousands more.
Inquire about ordering a limited edition copy (one size, 20 by 40 inches)

“Fleur d’Ellipse”
© 2006 Douglas McKenna. All rights reserved.
Fleur d’Ellipse is a fanciful recursive geometric design that is based on heptagonal subdivisions,
arranged elliptically in such a way as to seem almost flowerlike, and not quite symmetric. First drawn
in the early 1980's as a pen-plotter drawing, Fleur d’Ellipse contains both bold and delicate details,
arranged in ways that use tilings based on the silver ratio in an almost fern-like fractal texture.
See magnified detail here.
Inquire about ordering a small, medium, or large copy

“Interruption”
© 2011 Douglas McKenna. All rights reserved.
Interruption has an underlying combinatoric structure based on a newly discovered family of space-filling curve generators.
Inquire about ordering a small, medium, or large copy

“Moroccan Half-Dominos”
© 2017 Douglas McKenna. All rights reserved.
Moroccan Half-Dominos comprises six interlinking half-domino space-filling curves, first enumerated by the artist and presented in the eBook/app Hilbert Curves for iPads and ARM-based Mac computers.
See magnified detail here.
Inquire about ordering a small, medium, or large copy

“Peano Quartet”
© 2005 Douglas McKenna. All rights reserved.
Peano Quartet is one of McKenna's most visually intriguing works.
Based on a fundamental self-similar, space-filling, tiling construction he discovered in 2004,
the piece is composed of a simple, diagonal motif repeated at different
scales and orientations, mixing foreground with background, according to
its own structure. The work captures one's
visual imagination as it subdivides a square into what initially appear
to be four similar or identical parts, but are not. There are
optical illusion qualities to it as well. One's eye is fooled
into seeing parallel horizontal features as not parallel.
The piece evinces the all-important tension between symmetry and asymmetry
that McKenna feels is the hallmark of all successful mathematical art.
Inquire about ordering a small, medium, or large copy

“Platonic Dance”
(36" x 48" Black & White)
© 2006 Douglas McKenna. All rights reserved.
Platonic Dance is, like Peano Quartet, based on a repeated, simple diagonal geometric motif
in different sizes and with strong symmetrical and asymmetrical arrangements, reflecting a
deep self-referential structure within the square. Given the completely different visual feel of
this piece compared to the
Peano Quartet above, it is remarkable that both pieces can be dissected into
the exact same set of small square tiles.
Inquire about ordering a small, medium, or large copy

“Blade Rainer”
© 2006 Douglas McKenna. All rights reserved.
Blade Rainer is, like the above two, another in McKenna's B&W explorations of self-referential,
space-filling patterns within the square.
The imagery here arises out of basic combinatorial
constraints within the square and has tremendously strong vertical elements.
This piece is far more stark and foreboding
to the eye, with intimations of both skating blades on the right, and
bands of razor blades internally.
Inquire about ordering a small, medium, or large copy

“Pla(te Tec)tonic Dance”
© 2006 Douglas McKenna. All rights reserved.
Pla(te Tec)tonic Dance displays a strong tension between the binary subdvision of the square (one
set of fault lines) and the myriad diagonal elements that suffuse the image everywhere. It is one
of several related variations, the others of which are named Platonic Dances. It appears almost as
an abstract representation of horizontal sedimentary deposition over a different angled layer of
fractured (and fractal!) rock.
Inquire about ordering a small, medium, or large copy

“Golden Gnomon”
© 2007 Douglas McKenna. All rights reserved.
Golden Gnomon is a new, more accurately drawn version of a pen plotter drawing McKenna first made
back in 1985. It is based on a non-periodic Ammann tiling, which is in turn based on even and odd
powers of the square root of the golden ratio. Not surprisingly, one can even find the Fibonacci
numbers hidden in the design.
See magnified detail here.
Inquire about ordering a small, medium, or large copy

“Thirteenski”
© 2007 Douglas McKenna. All rights reserved.
Thirteenski is a base-13-based fractal space-filling curve that McKenna recently discovered.
This self-avoiding variation, with multiple scales, again exhibits a fascinating tension between symmetry and asymmetry,
with an almost African art quality to it. The name Thirteenski is a reference to the mathematician
Sierpinski, whose "Carpet" construction this abstract design "threads".
Inquire about ordering a small, medium, or large copy

“Synaptica”
© 2008 Douglas McKenna. All rights reserved.
Synaptica is a simple tile design, using square tiles of two colors, that is self-negative: if you rotate
it by 180 degrees, black and white tiles swap. The same is true for the component design repeated throughout.
This design is based upon a generalized Peano curve: the border between black and white tiles is a
simple continuous path. And the foreground and background have the same shape.
While the tiling pattern appears periodic, it is not (quite). It's called Synaptica because the repeated
motif reminded me of synapses, where some of them have a connective spark at the center. The pattern
is also reminiscent of Native American weavings, such as Navajo rugs with their geometric motifs.
Inquire about ordering a small, medium, or large copy

“Hepdragon Fire”
© 2005 Douglas McKenna. All rights reserved.
Hepdragon Fire illustrates a hidden asymmetric fractal embedded in a triangle derived
from the regular heptagon (seven-sided polygon). McKenna first created/discovered the Hepdragon in 1984.
The first pictures were single-color plotter drawings using custom line shading to accentuate the convergence.
This new version is built from thousands of similar triangles,
colored to evoke the energetic, fiery, jagged skin of a dragon-like figure, rearing a
self-similar head within a dark world. The triangles
converge from both the inside and the outside to the same shape.
See detail for the top of dragon head here.
Inquire about ordering a small, medium, or large copy

“Phiberspace”
© 2007 Douglas McKenna. All rights reserved.
Phiberspace is composed of over 42,000 copies, in various sizes, of the better golden rectangle specially chosen and colored so that
superpositions of them all lead the eye to see spirals upon spirals. The repeated rectangles a smaller scales are not themselves golden, but
each one is placed in a manner related to the Golden Ratio.
See magnified detail here.
Inquire about ordering a small, medium, or large copy